Power, Indices and Surds Questions for Competitive Exams

Power, Indices and Surds Questions for Competitive Exams. Important MCQ, selected from the previous year exam questions papers of SSC CGL, CPO, CHSL, Bank, UPSSSC and other govt jobs examinations for practice. topic wise question and answer of Power, Indices and Surds with solutions are very useful for upcoming competitive Examinations .

Power, Indices and Surds Questions

Finding the Largest and Smallest Values

Q.1: The greatest number among 3⁵⁰, 4⁴⁰, 5³⁰ and 6²⁰ is
a) 3⁵⁰
b) 4⁴⁰
c) 5³⁰
d) 6²⁰

Show Answer

Ans : b) 4⁴⁰
3⁵⁰ =(3⁵)¹⁰ = (243)¹⁰
4⁴⁰ = (4⁴)¹⁰=(256)¹⁰
5³⁰ = (5³)¹⁰ = (125)¹⁰
6²⁰ = (6²)¹⁰ = (36)¹⁰

Q.2: The greatest number among the following is $\frac 49, \sqrt{\frac {9}{49}}, 0.47, (0.7)^2$
a) $\frac 49$
b) $\sqrt{\frac {9}{49}}$
c) 0.47
d) $(0.7)^2$

Show Answer

Ans : d) $(0.7)^2$
$\frac 49$

=0.44
$\sqrt{\frac {9}{49}} = \frac37 = 0.43$

$(0.7)^2 = 0.49$

Q.3: Arranging the following in descending order:
$\sqrt[3]{4}, \sqrt 2, \sqrt[6]{3}, \sqrt[4]{5},$
a) $\sqrt[3]{4} > \sqrt[4]{5} > \sqrt 2 > \sqrt[6]{3}$
b) $\sqrt[3]{4} > \sqrt 2 > \sqrt[6]{3}>\sqrt[4]{5}$
c) $\sqrt 2 >\sqrt[3]{4} > \sqrt[6]{3}> \sqrt[4]{5}$
d) $\sqrt[6]{3} >\sqrt[4]{5} >\sqrt[3]{4}> \sqrt 2$

Show Answer

Ans : a) $\sqrt[3]{4} > \sqrt[4]{5} > \sqrt 2 > \sqrt[6]{3}$
$\sqrt[3]{4} = 4^\frac13 = (4^4) = (256)^\frac {1}{12}$

$\sqrt 2 = 2^\frac{1}{12} =(64)^\frac{1}{12}$

$\sqrt [6]3 = 3^\frac{1}{6} = (3^2)^\frac {1}{12} = (9)^\frac {1}{12}$

$\sqrt[4] 5 =5^{\frac14}= (5^3)^{ \frac{1}{12}} =(125)^\frac{1}{12}$

Q.4: The smallest among the numbers 2²⁵⁰, 3¹⁵⁰, 5¹⁰⁰, 4²⁰⁰ is
a) 2²⁵⁰
b) 3¹⁵⁰
c) 5¹⁰⁰
d) 4²⁰⁰

Show Answer

Ans : c) 5¹⁰⁰
2²⁵⁰ =(2⁵)⁵⁰ =(32)⁵⁰
3¹⁵⁰ = (3³)⁵⁰ = (27)⁵⁰
5¹⁰⁰ = (5²)⁵⁰ =(25)⁵⁰
4²⁰⁰ = (4⁴)⁵⁰= (256)⁵⁰

Q.5: Which is greater $\sqrt[3]2$ or $\sqrt3$ ?
a) $\sqrt[3]2$
b) $\sqrt3$
c) Equal
d) Can not be compared

Show Answer

Ans : $\sqrt3$
Cube of both the numbers are
$(\sqrt[3]2)^3 =2 \: \text {and} \: (\sqrt3)^3 = 3 \sqrt3$

Q.6: The smallest among $\sqrt[6]{12}, \sqrt[3]4, \sqrt[4]5, \sqrt3$ is
a) $\sqrt[6]{12}$
b) $\sqrt[3]4$
c) $\sqrt[4]5$
d) $\sqrt3$

Show Answer

Ans : c) $\sqrt[4]5$
LCM of 2,3,4 and 6 is 12
$\sqrt[6]{12}$

=(12)^1/6 =(12)^2/12 = (12²)^1/12 = (144)^1/12
$\sqrt[3]4$

= (256)^1/12
$\sqrt[4]5$

= (125)^1/12
$\sqrt3$

= (729)^1/12

Q.7: If X =(0.25)1\2, Y = (0.4)2, Z=(0.216)1/3, then
a) Y>X>Z
b) X>Y>z
c) Z>X>Y
d) X>Z>Y

Show Answer

Ans : c) Z>X>Y
X=(0.25)1/2 =0.5
Y= (0.4)2 = 0.16
Z = (0.216) = 0.6

Simplifying when the Root Values are given

Q.8: If $\sqrt {33} =5.745, \text {than the value of} \sqrt {\frac {3}{11}}$ is approximately.
a) 1
b) 0.5223
c) 6.32
d) 2.035

Show Answer

Ans : b) 0.5223
$\sqrt {\frac {3}{11}} = \sqrt {\frac {3\times 11}{11 \times 11}} = \frac {1}{11} \sqrt {33} = \frac{5.745}{11} = 0.5223$

Q.9: If $\sqrt 2 = 1.4142......$ is given, then the value of $\dfrac {7} {(3+\sqrt2)}$ correct up to two decimal places is :
a) 1.59
b) 1.60
c) 2.58
d) 2.57

Show Answer

Ans : a) 1.59
$\frac {7} {(3+\sqrt2)} = \frac {7} {(3+\sqrt2)} \times \frac {3-\sqrt2}{3-\sqrt2} = \frac {21-7\sqrt2}{9-2} =3-\sqrt2 = 3-1.4142 =1.59$

Q.10: Evaluate : $16\sqrt {\frac34} - 9\sqrt \frac 34 \: \: \: \text {if} \: \sqrt {12} = 3.46$
a) 3.46
b) 10.38
c) 13.84
d) 24.22

Show Answer

Ans : a) 3.46
$16\sqrt {\frac{3\times 4} {4\times4} } - 9\sqrt {\frac {4\times3}{3\times 3}}$

= $\frac {16}{4}\sqrt{12}-\frac 93 \sqrt {12}$

= $4 \sqrt{12} -3\sqrt{12} = \sqrt {12} = 3.46$

Rationalising or Prime Factor

Q.11: The number of prime factors in 6³³³ x 7²²² x 8¹¹¹
a) 1221
b) 1222
c) 1111
d) 1211

Show Answer

Ans : a) 1221
6³³³ x 7²²² x 8¹¹¹ = (2×3)³³³ x 7²²² x (2³)¹¹¹ = 2³³³ x 3³³³ x 7²²² x 2³³³
Total Prime Factor = 333+333+222+333= 1221

Q.12: The total number of prime factors in 4¹⁰ x 7³ x 16² x 11 x 10² is
a) 34
b) 35
c) 36
d) 37

Show Answer

Ans : c) 36
4¹⁰ x 7³ x 16² x 11 x 10²
= (2²)¹⁰ x 7³ x (2⁴)² x 11 x (5×2)²
= 2²⁰ x 7³ x 2⁸ x 11 x 5² x2²
=2³⁰ x 5² x 7³ x 11
Total Prime Factors = 30+2+3+1 = 36

Q.13: The rationalizing factor of $3 \sqrt3$ is
a) $\frac 13$
b) 3
c) -3
d) $\sqrt 3$

Show Answer

Ans : d) $\sqrt 3$
$3 \sqrt3 \times \sqrt3$

= 3 x 3 =9

Positive and Negative Exponent

Q.14: The quotient when 10¹⁰⁰ is divided by 5⁷⁵ is
a) 2²⁵ x 10⁷⁵
b) 10²⁵
c) 2⁷⁵
d) 2⁷⁵ x 10²⁵

Show Answer

Ans : d) 2⁷⁵ x 10²⁵

Q.15: If 3^x+8= 27^2x+1 , then the value of x is :
a) 7
b) 3
c) -2
d) 1

Show Answer

Ans : d) 1
3^x+8= 27^2x+1 = (3³)^2x+1 =3^6x+3
x+8 =6x + 3
5x = 5, x=1

Q.16: (36)^1/6 is equal to
a) 1
b) 6
c) $\sqrt 6$
d) $\sqrt[3]{6}$

Show Answer

Ans : $\sqrt[3]{6}$
(36)^1/6 = (6²)^1/6 = 6^1/3 = $\sqrt[3]{6}$

Based on Square Root Series : Power, Indices and Surds Questions

Q.17: The value of the expression is :
$\sqrt {6+\sqrt {6+\sqrt{6+ ...........}}}$
a) 5
b) 3
c) 2
d) 30

Show Answer

Ans : b) 3
Let $\sqrt {6+\sqrt {6+\sqrt{6+ ...........}}} = x$

Squaring both side
$6 + \sqrt {6+\sqrt {6+\sqrt{6+ ...........}}} = x^2$

= $x^2 = 6+x$

= $x^2 - 3x +2x -6 = 0$

= $(x-3)(x-2) = 0$

= $x = 3$

Q.18: $\dfrac {\sqrt{10+ \sqrt{25+ \sqrt{108+ \sqrt{154+ \sqrt{225}}}}}} {\sqrt[3]8}$ = ?
a) 4
b) 2
c) 8
d) $\frac12$

Show Answer

Ans : b) 2
$\dfrac {\sqrt{10+ \sqrt{25+ \sqrt{108+ \sqrt{154+ 15}}}}} {2}$

= $\dfrac {\sqrt{10+ \sqrt{25+ \sqrt{108+ \sqrt{169}}}}} {2}$

= $\dfrac {\sqrt{10+ \sqrt{25+ \sqrt{108+ 13}}}} {2}$

= $\dfrac {\sqrt{10+ \sqrt{25+ 11}}} {2}$

= $\dfrac {\sqrt{10+ 6}} {2} = \dfrac 42 = 2$

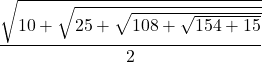
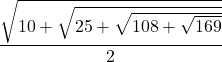
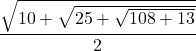
Power, Indices and Surds Questions in Hindi – NRA STUDY

Leave a Comment Cancel Reply